Ar žinote apie ESP32 ADC reguliavimą?: 29 žingsniai

2024 Autorius: John Day | [email protected]. Paskutinį kartą keistas: 2024-01-30 10:47

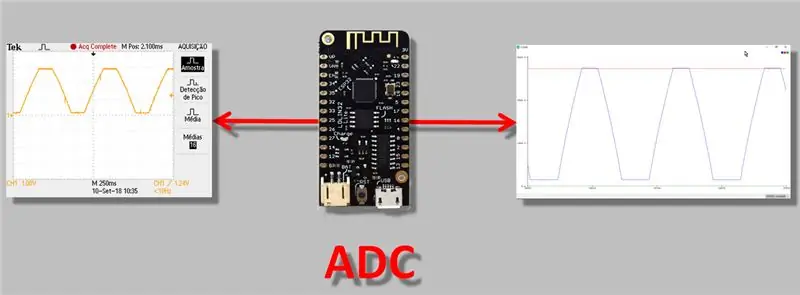
Šiandien aš kalbėsiu apie labiau techninę problemą, tačiau manau, kad kiekvienas, dirbantis su ESP32, turėtų žinoti: ADC (analoginio-skaitmeninio keitiklio) skaitymo koregavimo problema. Manau, kad tai svarbu, nes atliekant „matavimą“, ypač naudojant instrumentą su analogine išvestimi, turite būti visiškai tikri, kad rodmenys atliekami teisingai.

Todėl šiandienos vaizdo įraše atliksime matavimus naudodami ESP32 „analoginį skaitmeninį keitiklį“, stebėsime konversijos neatitikimus ir taikysime ADC koregavimo / kalibravimo metodą.

1 veiksmas: kas yra AD keitiklis?

AD keitiklis yra grandinė, galinti analoginį (nuolatinį) kiekį paversti skaitmeninėmis (diskrečiomis) reikšmėmis. Ką tai reiškia? Tai reiškia, kad nors skaitmeninės vertės gali prisiimti tik atskiras reikšmes, sudarytas iš nulių ir vienetų derinio, analoginis kiekis gali prisiimti bet kokią intervalo vertę. Pavyzdžiui, jei išmatuotume idealaus AA elemento įtampą, galėtume rasti bet kokią vertę tarp 0V ir 1,5V, nes tai yra analoginis kiekis. Idealios lempos išėjimo būsena turi turėti tik dvi būsenas (išjungta arba įjungta), o tai yra diskretiškas dydis. Kadangi mikrovaldikliai dirba pagal šią diskretišką logiką, mums reikia grandinės, galinčios analoginį kiekį paversti skaitmeniniu (arba diskrečiu).

2 žingsnis: naudojami ištekliai

• Viena „Lolin32 Lite“kortelė v1.0.0

• Tektronix TDS1001C osciloskopas, skirtas fiksuoti

• Vienas ESP32 USB kabelis

• Hantek DSO4102C osciloskopas kaip signalų generatorius

3 žingsnis: ESP32 ADC

Remiantis „Espressif“duomenimis, ESP32 mikroschemų matavimo rezultatai gali skirtis nuo +/- 6% nuo vieno lusto iki kito.

Be to, konversija NĖRA linijinio atsakymo į kiekvieną turimą skaitymo diapazoną. „Espressif“pateikia kalibravimo metodą ir siūlo vartotojams įgyvendinti kitus metodus, jei mano, kad tai būtina norint pasiekti norimą tikslumą.

Mes atliksime duomenų rinkimą ir iš to parodysime ADC atsakymus bei matematinio proceso pritaikymo pavyzdį, kad perskaitytume koregavimą.

Yra keli (paprastesni ar sudėtingesni) būdai, kaip atlikti šiuos pataisymus. Jūs turite įvertinti, kas labiausiai tinka jūsų projektui.

Čia pateiktas pavyzdys bus iliustratyvus ir bandys išspręsti įdomius dalykus, kuriuos galima pastebėti atliekant koregavimus.

4 žingsnis: naudojama grandinė

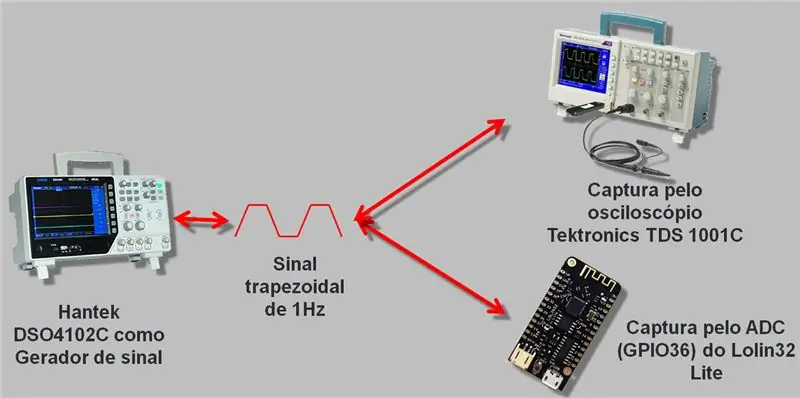
Naudojau osciloskopą su signalų generatoriumi, kuris eina iki 25 MHz, „Hantek DSO4102C“. Mes sukūrėme bangą, kurią skaitė ESP A / D ir osciloskopas. Surinkti duomenys buvo įrašyti csv ir skaičiuoklėje, kurią paliksiu straipsnio pabaigoje atsisiųsti.

5 žingsnis: naudojamas ženklas

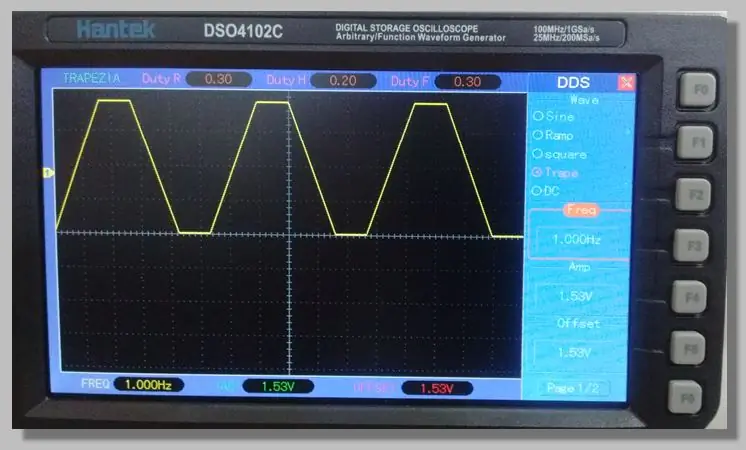
Mes pasirinkome žemo dažnio trapecijos signalą, kuris leidžia pasiekti rampas, einančias per visą konversijos diapazoną. Dėl to ant šių rampų galima paimti daug mėginių.

6 žingsnis: Osciloskopu gauti duomenys

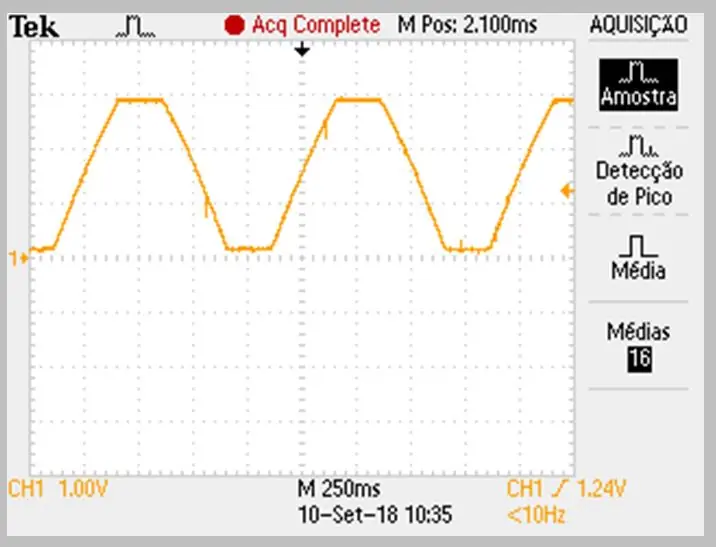
Fotografavimo vaizdas buvo atliktas osciloskopu. Duomenys buvo saugomi csv faile. Atkreipkite dėmesį į nedidelį signalo kylančių ir krintančių rampų kreivumą.

7 žingsnis: Osciloskopu gauti duomenys (csv failas „Excel“)

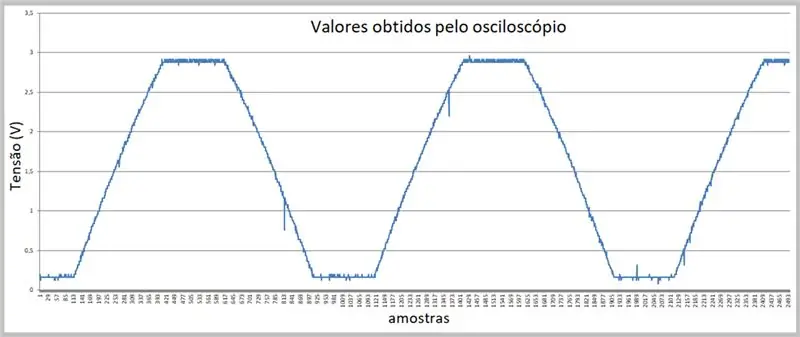
Čia turime pavyzdžių.

8 žingsnis: ADC gauti duomenys

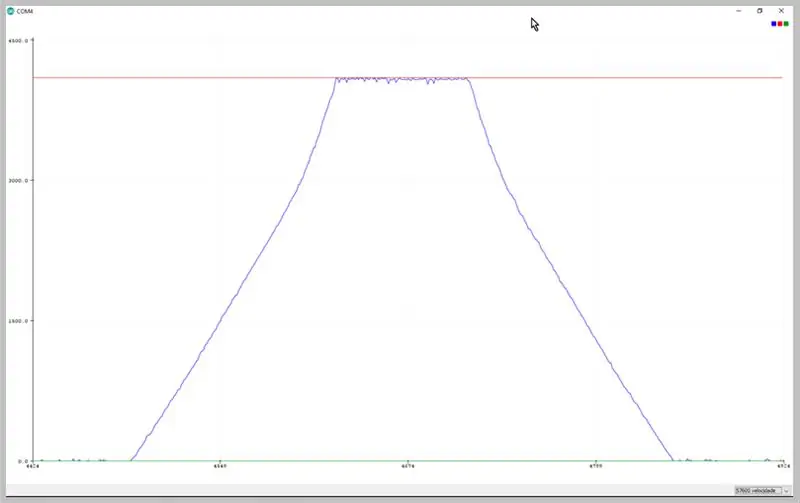
Keisdami serijos perdavimo greitį, galime peržiūrėti ADC užfiksuotus duomenis. Stebėkite trapecijos signalo deformaciją.

Duomenys, pastebėti naudojant „Arduino IDE“serijos braižytuvą

9 žingsnis: ADC gauti duomenys - „Excel“

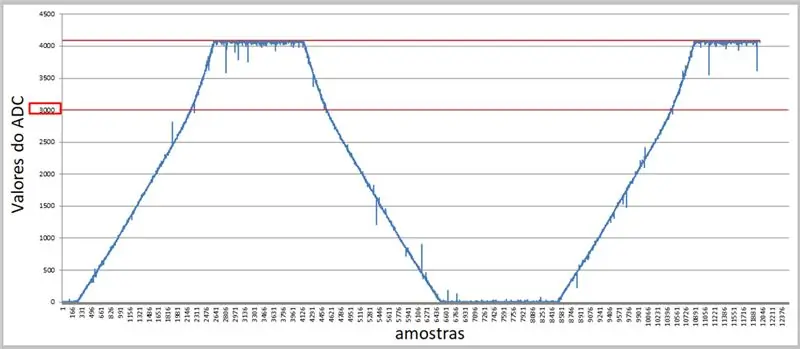
Naudodami didesnį tarifą ir nuoseklųjį terminalą, mes galime užfiksuoti reikšmes ir pritaikyti jas „Excel“, kad galėtume palyginti.

10 žingsnis: laipiojimo rampų palyginimas

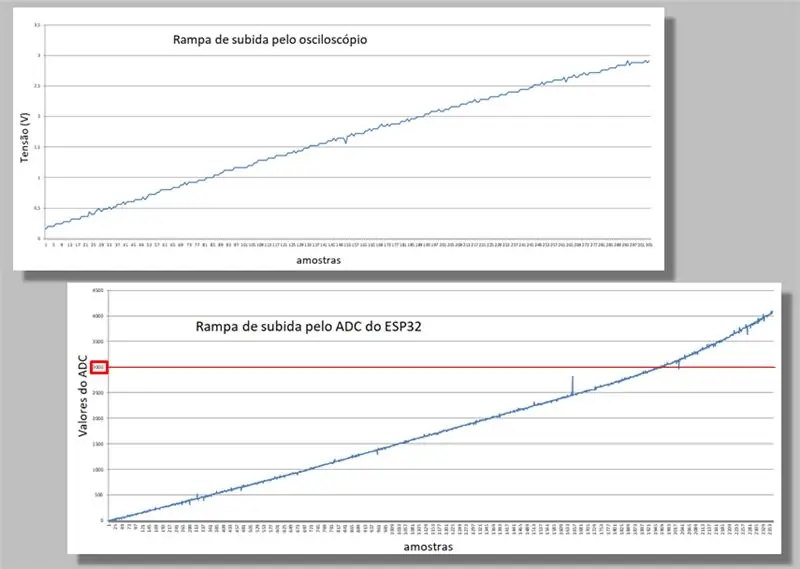
Palyginame dviejų laipiojimo rampas.

Atkreipkite dėmesį į abiejų rampų kreivumą.

Taip pat atkreipkite dėmesį, kad toje pačioje rampoje turime daug daugiau ESP32 mėginių nei iš osciloskopo.

11 veiksmas: mėginių skaičiaus sulyginimas

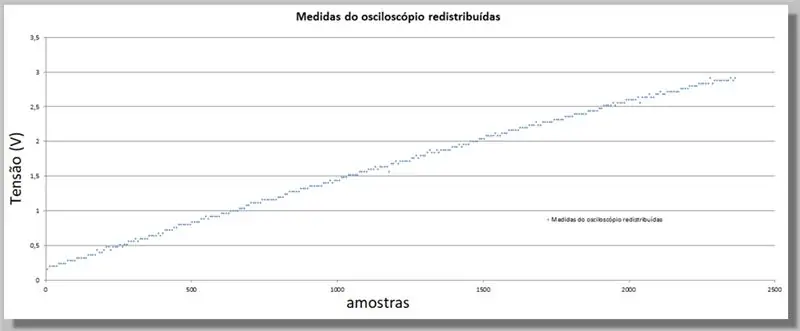
Kadangi ESP32 pateikė daugiau mėginių nei osciloskopas, turime šias vertes sulyginti, nes jos bus rodiklis, leidžiantis palyginti dvi kreives.

Norėdami tai padaryti, atliksime tiesioginį palyginimą.

Turime 305 osciloskopo rampos pavyzdžius ir 2365 ADC rampos pavyzdžius.

Kadangi rampos yra to paties diapazono, galime pasakyti, kad kiekvienam osciloskopui turime maždaug 7,75 ADC pavyzdžių.

Padauginus kiekvieno osciloskopo mėginio indeksą, kreivė yra ta pati, tačiau indeksai atitinka ADC ir perskirstytus duomenis.

Norėdami užpildyti trūkstamus naujų pozicijų duomenis, pritaikysime kreivę, kuri statistiškai atitinka žinomus duomenis.

12 žingsnis: užpildykite spragas - tendencijų liniją

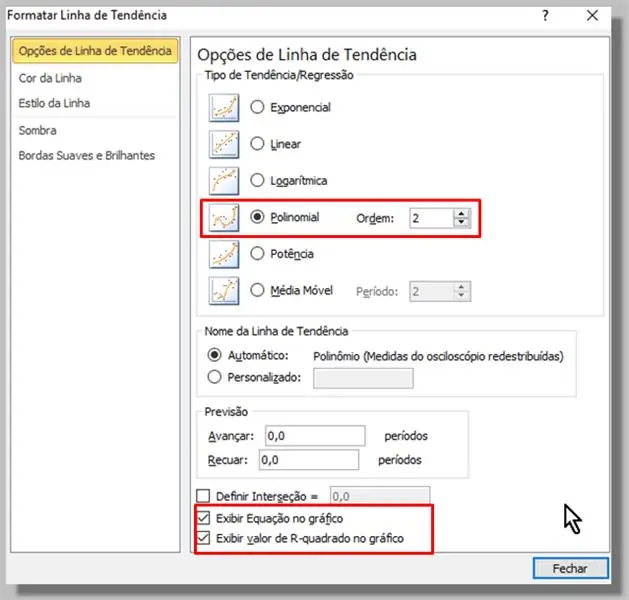
Pasirinkę žinomus duomenis (mėlynus taškus), spustelėdami ir spustelėdami dešiniuoju mygtuku, pasirenkame: „Pridėti tendencijų eilutę …“

Pasirodžiusiame lange pasirenkame polinominį tipą (užteks 2 eilės).

Taip pat patikrinome parinktis „Peržiūrėti diagramos lygtį“ir „Rodyti diagramos R kvadrato reikšmę“.

Spustelime „Uždaryti“.

13 žingsnis: užpildykite spragas - 2 laipsnio polinominė kreivė

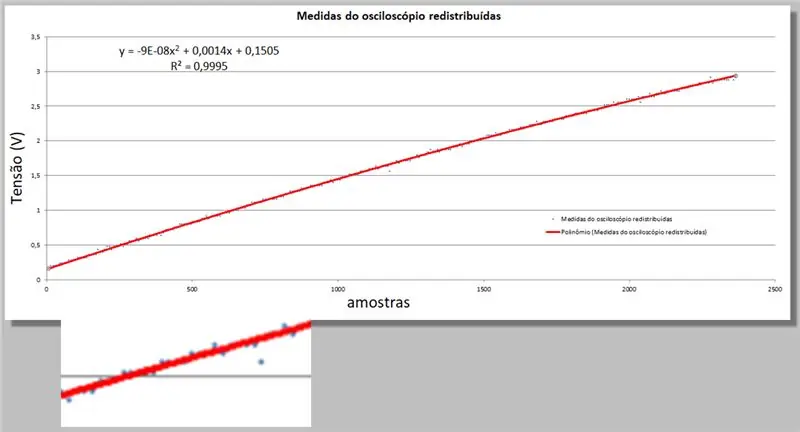
„Excel“suteikia mums dvi naujas informacijos dalis; antros eilės lygtis, kuri geriausiai atitinka duomenis, ir R kvadrato lygtis, kuri kiekybiškai įvertina šį adekvatumą.

Tiesiog nepamirškite, kad kuo arčiau 1, tuo tikslesnė lygtis.

Nesigilinkime į matematiką, naudokime ją tik kaip įrankį.

14 žingsnis: užpildykite spragas - įvertinkite funkciją

Užpildykime atrankos spragas duomenimis, gautais pagal lygtį. Ir tada palyginkite juos tašku po taško.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Osciloskopo įtampa = -9E -08 * indeksas2 + 0, 0014 * indeksas + 0, 1505

15 žingsnis: Osciloskopo įtampos konvertavimas į lygiavertę vertę, palyginti su ADC

Pasinaudokime tuo, kad taip pat pakeistume osciloskopo įtampos vertę į lygiavertę ADC vertę.

Kadangi didžiausia ESP32 ADP gauta vertė buvo 4095, o tai atitinka to paties indekso 2,958 V rodmenį, galime pasakyti, kad:

Kiekvienas osciloskopo matavimo voltas yra maždaug 1384,4 AD vienetų. Todėl visus osciloskopo matavimus galime padauginti iš šios vertės.

16 žingsnis: dviejų gautų rampų palyginimas

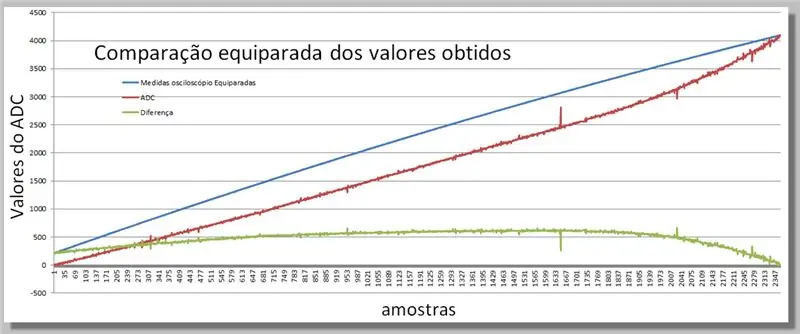
Vizualizuokite skirtumus, gautus per du skaitymus.

17 veiksmas: ADC skaitymo skirtumo (ERROR) elgesys

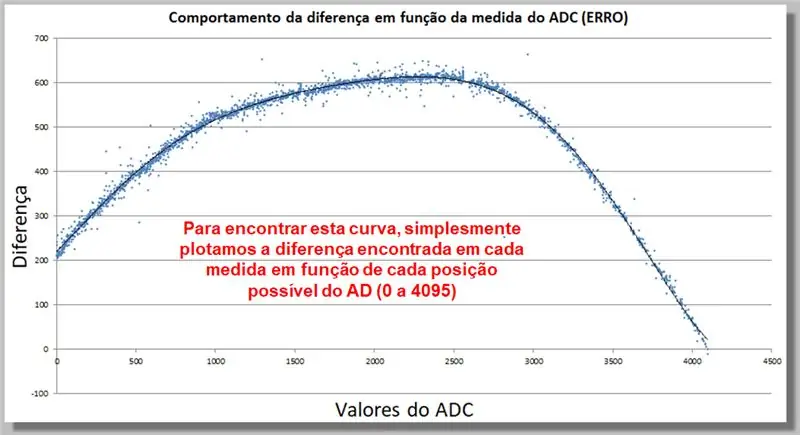
Žemiau pateikta kreivė rodo, kaip ADC rodmenų skirtumas veikia kaip matavimo funkcija. Šis duomenų rinkimas leis mums rasti korekcijos funkciją.

Norėdami rasti šią kreivę, mes paprasčiausiai nubraižome kiekvienoje priemonėje rastą skirtumą kaip kiekvienos galimos AD padėties funkciją (nuo 0 iki 4095).

18 veiksmas: ADC skaitymo skirtumų elgesys - korekcijos funkcijos paieška

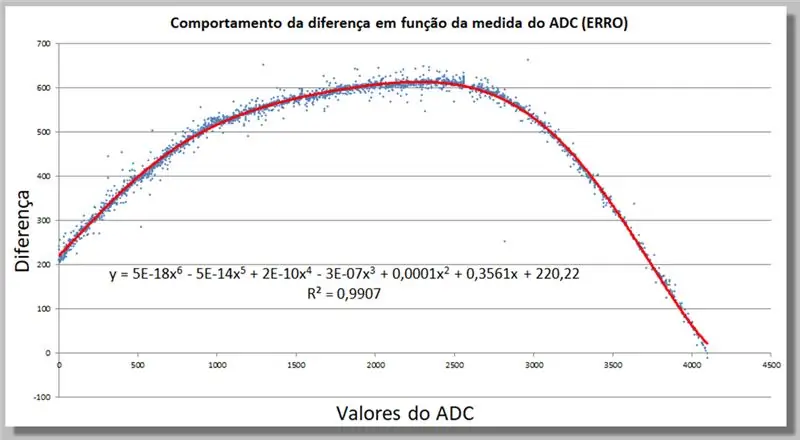
Koregavimo funkciją „Excel“galime nustatyti pridėję aukštesnio lygio tendencijų liniją, kol ji pakankamai dera su mūsų duomenimis.

19 veiksmas: kitos programinės įrangos naudojimas

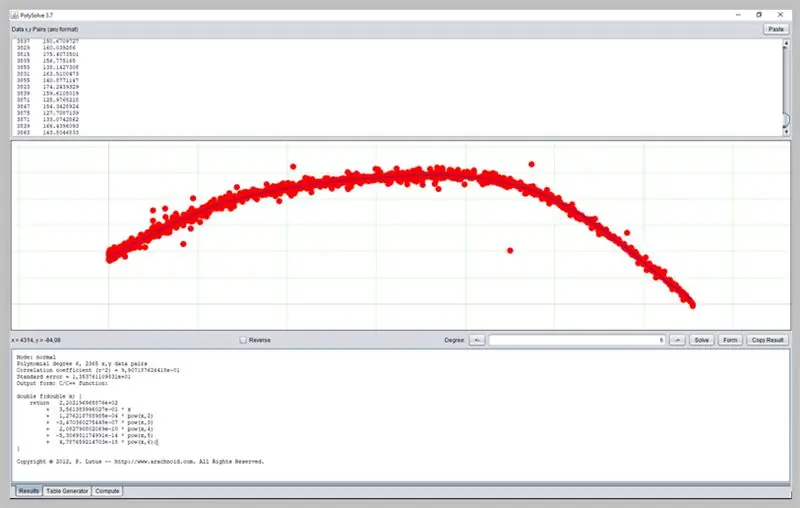
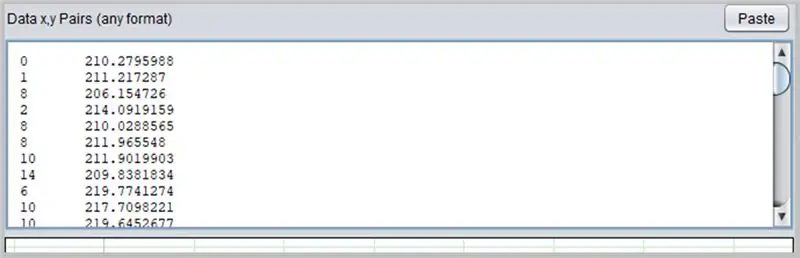
Kita įdomi programinė įranga kreivėms nustatyti yra „PolySolve“, kurią galima naudoti tiesiogiai nuorodoje: https://arachnoid.com/polysolve/ arba atsisiųsti kaip „Java“programą.

Tai leidžia taikyti aukštesnio laipsnio polinomines regresijas ir pateikti suformatuotą funkciją bei kitas funkcijas.

Norėdami jį naudoti, tiesiog įveskite duomenis į pirmąjį teksto lauką. Duomenys turi atitikti tvarką X, Y, atskirti kableliu arba skirtuku. Būkite atsargūs, teisingai naudodami tašką kaip dešimtainį tašką.

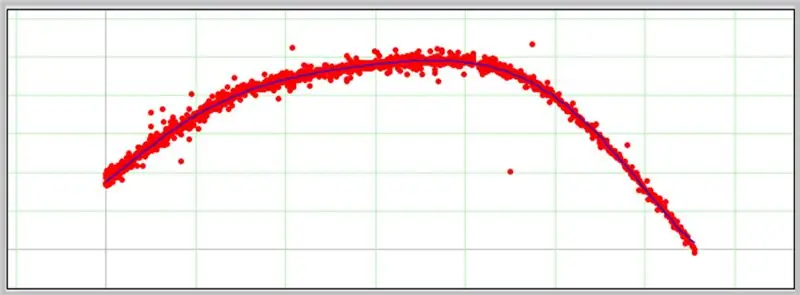
Diagrama bus rodoma kitame lange, jei įvesti duomenys bus tinkamai suformatuoti.

Štai kaip vyko mūsų ADC klaidų kreivė.

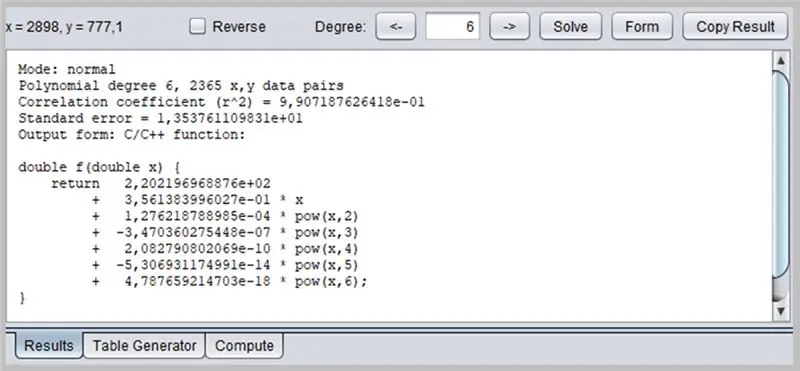
Šiame lange bus pateiktas regresijos rezultatas, įskaitant funkcijos adekvatumo duomenis, kurie savo ruožtu gali būti suformatuoti keliais būdais: kaip C / C ++ funkcija, koeficientų sąrašas, funkcija, parašyta „Java“ir kt.

Pastaba: atkreipkite dėmesį į dešimtainius skyriklius

20 veiksmas: konstantos ir sąranka ()

Čia atkreipiu dėmesį į GPIO, naudojamą analoginiam fiksavimui. Inicijuoju nuoseklųjį prievadą, taip pat kaištį, nustatytą analoginiam fiksavimui.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Iniciciando a porta serial somente para debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

21 veiksmas: ciklas () ir taisymo funkcija

Mes fiksuojame sureguliuotą įtampą ir spausdiname vertes su teisingomis korekcijomis arba be jų.

void loop () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada // Serial.print (valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serijinis.println (0); // cria uma linha para marcar o valor mínimo de 0}

Atkreipkite dėmesį į 12 eilutę, kad turime galimybę spausdinti duomenis, pridėdami skirtumo funkciją f (analog_value).

22 veiksmas: „PolySolve Correction“funkcijos naudojimas

Čia mes naudojame „PolySolve“funkciją „Arduino IDE“viduje.

/* Režimas: normalus polinominis 6 laipsnis, 2365 x, y duomenų poros Koreliacijos koeficientas (r^2) = 9, 907187626418e-01 Standartinė paklaida = 1, 353761109831e+01 Išvesties forma: C/C ++ funkcija: Copyright © 2012, P. Lutus - https://www.arachnoid.com. Visos teisės saugomos. */ double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Atkreipkite dėmesį į kablelio po taško pakeitimą kaip dešimtainį skyriklį.

23 veiksmas: fiksuokite taisydami - braižytuvo serija

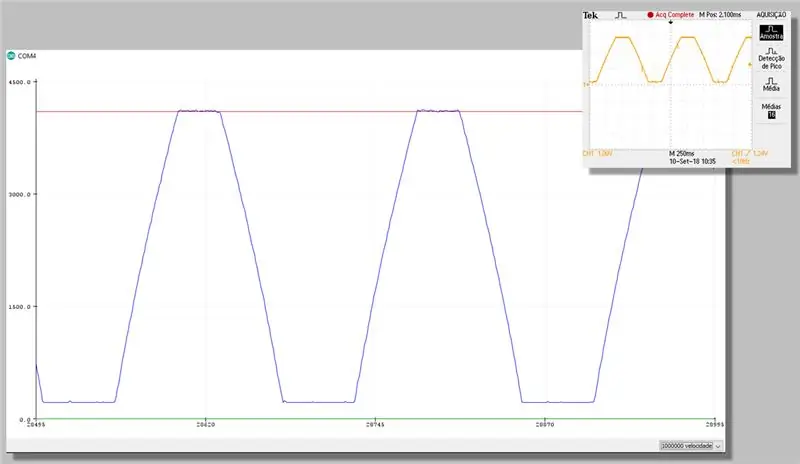
24 žingsnis: skaičiavimo išlaidos

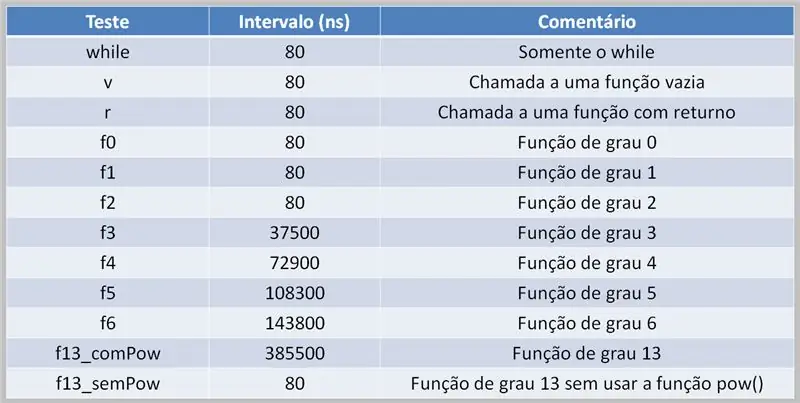
Norint atlikti daugianarius skaičiavimus, būtina, kad procesorius atliktų šią užduotį. Tai gali sukelti vėlavimą vykdyti, priklausomai nuo šaltinio kodo ir turimos skaičiavimo galios.

Čia matome bandymo, kuriame naudojami kelių laipsnių daugianariai, rezultatų lentelę. Atkreipkite dėmesį į skirtumą tarp laiko, kai buvo naudojama „pow“() funkcija, o kada - ne.

25 veiksmas: bandymo kodas - sąranka () ir ciklo pradžia ()

Čia mes turime kodą, naudojamą mūsų bandyme.

void setup () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000,0; // quantidade de chamadas float contador = 0.0; // contador de chamadas

26 veiksmas: bandymo kodas - ciklas () ir apdorojimas

Naudojau funkciją micros (), kad gaučiau vertę mikrosekundėmis.

// ============= inicia o o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============= baigtas procesas

27 veiksmas: bandymo kodas - ciklas () - rezultatai

Palyginimui spausdiname iš 13 klasės funkcijos grąžintą vertę su ir be POW, taip pat apdorojimo intervalą.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (agora, 6); }

28 žingsnis: bandymo kodas - naudojamos funkcijos

Tuščios 0 ir 1 laipsnio funkcijos (tik su grąžinimu).

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 dviguba f1 (dviguba x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x; }

2, 3 ir 4 klasių funkcijos.

// FUNÇÃO DE GRAU 2double f2 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)) + 2.082790802069e-10 * pow (x, 4); }

5 ir 6 klasių funkcijos.

// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

13 laipsnio funkcija naudojant POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

13 laipsnio funkcija nenaudojant POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

29 žingsnis: failai

Atsisiųskite failus:

PDF

AŠ NE

Skaičiuoklė