
Turinys:
- Autorius John Day day@howwhatproduce.com.
- Public 2024-01-30 10:46.
- Paskutinį kartą keistas 2025-01-23 14:59.
Sekite daugiau autoriaus:


Klasėje mes dažnai naudojame chronometrą švytuoklės eksperimentui arba paprastam harmoninio judesio eksperimentui. Čia yra iššūkis, ar galime sukurti tikrą jo judėjimo grafiką ir pamatyti, kas yra momentinė kampinė padėtis ir greitis, tai daug daugiau informacijos ir linksmybių.
Pirmasis klausimas, mes turime nuspręsti, kad švytuoklės korpusas yra nesvarus laidas arba standus vienodas strypas. Atrodo, kad laidinis metodas yra lengvesnis. Remdamasis vienos statybos praktika, turiu tokius kompromisus: Lengviausias būdas pakabinti švytuoklės sistemą gali būti pakabintas prie viršutinio durų krašto. Tai suteikia jūsų ~ 2 m švytuoklės ilgį neatliekant jokių konstrukcinių statybos darbų. Tačiau reikia, kad sūpynės neliestų durų paviršiaus, o tai tiesiog sugadina visą eksperimentą. Taigi jo sukimosi plokštuma turi būti tiksliai lygiagreti jūsų sienos/durų paviršiui. Nesvarus laidas paprastai būna plonas, jis gali lengvai suktis ir apsunkina svyravimo kampo matavimą. Mes norime naudoti vieną matavimą, kad pavaizduotume svyravimo būseną. Plonas laidas, pvz., Žuvies virvė, gali būti elastingas ir ištemptas, o tai daro įtaką vienai iš svarbiausių mūsų matuojamų konstantų, naudojamų lygtyje, tai yra švytuoklės ilgis. Kai kuriuos taip pat gali paveikti temperatūra. Virvės gale kabanti svorio masė turi būti pakankamai sunki, kad virvės svoris taptų nereikšmingas. Komentuokite, jei sutinkate ar nesutinkate su jais arba turite kitų dizaino kompromisų idėjų. Norėdami ištirti šią problemą, mums reikia prietaiso, kuris yra toks lengvas, kad į jo svorį galima nekreipti dėmesio, ir mes vis dar traktuojame švytuoklę kaip standų vienodą strypą. Aš naudoju COTS nešiojamą elektroninį valdiklį, kuris „Bluetooth“ryšiu mums pateikia giroskopo, akselerometro ir kampo informaciją. Šie matavimai bus saugomi mobiliojo telefono programos duomenų faile. Po to mes analizuosime savo paprasto harmoninio judesio eksperimento duomenis. Skaitinė analizė sutelkta į šias temas: 1) numatyti švytuoklės svyravimo periodą 2) programuojamai surinkti švytuoklės paprastų harmoninių judesių eksperimento duomenis 3) naudoti kmean, kad sugrupuotų duomenis ir pašalintų pašalines vertes analizės procese 4) naudokite trumpo laiko FFT, kad įvertintumėte švytuoklės virpesių dažnis
Prekės
„Bluetooth“matavimo aparatas
„Android“telefono programa: eikite į „Google Play“parduotuvę, ieškokite M2ROBOTS ir įdiekite valdymo programą. Jei sunku pasiekti „Google Play Store“, apsilankykite mano asmeniniame pagrindiniame puslapyje, kur rasite alternatyvų programos atsisiuntimo būdą
medinis strypas
keletas 3D spausdintų dalių
pjūkleliai ar panašios metalinės medžiagos
1 žingsnis: kas yra švytuoklė? Kaip jį modeliuoti?
Yra daug straipsnių ir knygų, pristatančių švytuoklės lygties išvedimą, įskaitant jūsų mokymo programos fizikos knygą. Tokio turinio gali būti geriau nekartoti čia. Čia pateikiama tik galutinė išvada dėl „paprasto harmoninio judesio“. Kad žinotume švytuoklės laikotarpį, mums tereikia žinoti švytuoklės ilgį, pažymėtą „l“, metrais.
Jei esame pagrįstai tikri, kad svoris beveik visiškai yra besisukančio virvelės, pakabintos šarnyre, gale, o švytuoklė svyruoja mažais kampais θ, tarkime, mažiau nei 15 °, tokios švytuoklės laikotarpį T1 sudaro:
T1 = 2*pi*(l/g)^0,5
g = gravitacijos pagreitis, maždaug 9,8 m/s^2
Jei besvorį laidą pakeičia standus vienodas strypas, kurio ilgis vėl yra l, jo paprastas harmoninis judėjimo laikotarpis T2 yra T1 = 2*pi*(2l/3g)^0,5
Efektyviai jis turi tą patį laikotarpį kaip nesvari virvės švytuoklė, kuri yra du trečdaliai standaus vienodo strypo ilgio.
Tai yra fonas, ir mes galime pradėti rengti savo eksperimentą.
2 žingsnis: Paruoškite techninės įrangos kūrimo dalis



Norėdami sukurti švytuoklės struktūrą, 3D spausdiname kai kurias dalis ir perdirbame tai, ką jau turime. Bendra švytuoklės struktūra parodyta 1 pav. Tai 3D spausdinimo dalių mišinys kartu su kai kuriomis rankų darbo detalėmis ir ilgu medžio strypo gabalu iš „Lowe“.
2 pav. 3D spausdinta dalis yra pakabinta ant viršutinio durų krašto, nes mūsų durys yra lengvai plokščias paviršius, kurį galime pakabinti. STL failo atsisiuntimo nuoroda:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Žalia 3 paveikslo dalis sujungia medinį strypą su ašmenimis, o ašmenys yra ant dviejų bėgių dalių, sumontuotų ant ankstesnės 3D spausdintos durų pakabos. STL failo atsisiuntimo nuoroda:
Dvi bėgelio dalys pagamintos sulaužant seną pjūklo diską per pusę, žr. 4 pav. 2 pav. Esanti dalis paruošė jiems tinkamą plyšio dydį. Idealiu atveju mes galime padaryti „V“formos išpjovą tuose dviejuose pjūkleliuose, naudodami dildę. „V“formos išpjovų viduje gali tilpti pakankamai aštrus metalas, pvz., Vieno krašto skutimosi peiliukas arba bet kokia rankų darbo metalo detalė. Priežastis, kodėl mums reikia mažesnio kontaktinio ploto, yra sumažinti kinetinę energiją, prarastą siūbuojant.
Paskutinė 3D spausdinta dalis 5 pav. Yra mažas dėklas elektroniniam matavimo prietaisui laikyti.
Atsisiuntimo nuoroda:
„Bluetooth“matavimo aparatas generuoja kampo įvertinimą, giroskopo matavimą ir akselerometro matavimą. Visi šie duomenys mums prieinami per „Bluetooth“belaidį ryšį.
Mes atliksime kelis eksperimentus, panaudodami šį aparatą skirtingoje švytuoklės rankos padėtyje ir pamatysime skirtumus.
3 veiksmas: eksperimento duomenų rinkimas



Prieš analizuojant gautą duomenų rinkinį, yra du galimi eksperimentinio duomenų rinkimo metodai:
1) Naudokite „Android“telefono programą, nurodytą reikalavimų skyriuje, kad užregistruotumėte visus aparato atliktus matavimus į duomenų failą, saugomą jūsų telefono SD kortelėje. Galime nukopijuoti failą ir apdoroti informaciją.
2) Naudokite „Bluetooth“palaikantį kompiuterį, asmeninį kompiuterį, nešiojamąjį kompiuterį arba „RaspberryPi“mini kompiuterį, kad užmegztumėte „Bluetooth“ryšį su aparatu ir perskaitytumėte duomenis realiuoju laiku arba neprisijungę.
Kiekvienam metodui yra ir privalumų, ir trūkumų, mes išbandysime abu ir pasakysime skirtumą tarp šio pamokymo.
Taikant (1) metodą naudojant „Android“programą, kai būsime „Android“programos valdymo sąsajoje, telemetrijos duomenys, siunčiami iš „Bluetooth“matavimo aparato į „Android“telefoną, bus įrašyti į duomenų katalogo failą, pavadintą m2flightDatayyyymmdd_hhmmss.txt. Jį galima rasti „Android“telefono aplanke „Atsisiųsti/m2LogFiles“. Aplankas „Atsisiųsti“yra iš anksto esantis jūsų telefono „Android“OS aplankas, o „m2LogFiles“yra programos sukurtas aplankas. Failo pavadinimo turinys yyyymmdd_hhmmss yra būdas užkoduoti eksperimento pradžios laiką (metus, mėnesį, dieną, valandą, minutę ir sek.) Failo pavadinime.
Kiekviena žurnalo failo eilutė yra vienas įrašas. Jis prasideda įvykio laiko žyma, preambulės eilute „eam:“, po kurios eina 4 tripletiniai duomenys, kurie yra:
Akselerometro XYZ ašies nuskaitymas neapdorotų jutiklių aparatinės įrangos registro skaitymo reikšmėse
Giroskopo XYZ ašies nuskaitymas neapdorotų jutiklių aparatinės įrangos registro atkūrimo reikšmėse
Magnetometro XYZ ašies nuskaitymas neapdorotų jutiklių aparatinės įrangos registro atkūrimo reikšmėse
laive apskaičiuotas Roll/Pitch/Raw laipsnis
Duomenų failas, sukurtas naudojant kompiuterinę „python“programą, naudos identišką duomenų failo formatą, todėl programa, kurią naudojame duomenų analizės etape, netrukdys duomenų šaltiniui, kurį sukuria mūsų „python“programa arba „Android“programa.
Pradėkime koduoti naudodami (2) metodą.
Norint sąveikauti su „Bluetooth“matavimo aparatu, pateikiami dviejų tipų SDK:
1) Python SDK, kurį galima įdiegti naudojant „pip3 install m2controller“, naudojama kalba „python3“. Vartotojo programos kodo pavyzdžiai saugomi https://github.com/xiapeiqing/m2robots/tree/maste… Šiame eksperimente naudosime „python“scenarijų pendulum1.py
2) „Java SDK“, kuri nenaudojama šioje instrukcijoje, nes norime vėliau vizualizuoti ir analizuoti įgytus švytuoklės duomenis, o tai gali užtrukti šiek tiek daugiau pastangų, kad galėtume programuoti „Java“.
„Python3“duomenų rinkimo programos šaltinio kode yra daug komentarų apie kodo funkcionalumą. Čia pateikiamas šaltinio kodo momentinis vaizdas.
#!/usr/bin/env python#-*-kodavimas: UTF-8-*-iš „m2controller“importuoja „m2controller“iš „m2controller“importo m2
requestExit = Netiesa
################################################################
#norime naudoti tą patį žurnalo failų pavadinimo susitarimą, kad duomenų analizės modulis pendulum2.py galėtų būti agnostinis, kaip gauname žurnalo duomenų failą ################# #############################################. m2flightData%s.txt "%(datetime.datetime.fromtimestamp (time.time ()). strftime ('%Y%m%d_%H%M%S')) dataLogfile = atviras (žurnalo failo pavadinimas," w ")
def signal_handler (sig, frame):
visuotinė užklausaExit print ('naudotojas Ctrl-C norėdamas išeiti iš programos vykdymo') requestExit = Tikras signalas.signal (signal. SIGINT, signal_handler)
################################################################
#kai visi matavimo duomenys tampa prieinami 20 Hz dažniu, ši „atgalinio ryšio“funkcija bus iškviesta ############################## ################################## def callbackfunc (telemetrija): strTimeStamp = datetime.datetime.fromtimestamp (time.time ()). strftime ('%H:%M:%S.%f') [:-3] dataStr = "%s, eam:%d,%d,%d,%d,%d,%d, %d, %d, %d, %2.1f, %2.1f, %2.1f / n " %(strTimeStamp, telemetrija ['m_fAccelHwUnit'] [0], telemetrija ['m_fAccelHwUnit'] [1], telemetrija ['m_fAccelHwUnit'] [2], telemetrija ['m_fGyroHwUnit'] [0], telemetrija ['m_fGyroHwUnit'] [1], telemetrija ['m_fGyroHwUnit'] [2], telemetrija ['m_fMat 'm_fMagHwUnit'] [1], telemetrija ['m_fMagHwUnit'] [2], telemetrija ['m_fRPYdeg'] [0], telemetrija ['m_fRPYdeg'] [1], telemetrija ['m_fRPYdeg'] [2] # ############################################### #############mes atspausdiname duomenų eilutę ekrane ir įrašome į žurnalo failą ###################### ######## dataStr)
################################################################
#inicijuokite valdiklį, nepamirškite nustatyti lauko „BleMACaddress“kaip jūsų įrenginio MAC adreso ################################ ################################TODO: inicijuokime „BleMACaddress“, jei nenustatė naudotojas. controller = m2controller. BleCtrller (m2Const.etDebian, callbackfunc, usrCfg. BleMACaddress) controller.connect () o tiesa: ######################### ####################################### ##################### AMBBB wait wait wait wait #######################ba AMBB,, APPLT aparatas ################################################ ############### controller.m_CommsTunnel.waitForNotifications (1.0) if requestExit: ###################### ########################## ############### ############################################### ############## controller.stop () dataLogfile.close () break
################################################################
#duomenų rinkimas baigtas, dabar analizuosime žurnalo duomenis #################################### ######################### pendulum2.parseDataLogFile (žurnalo failo pavadinimas)
Norėdami gauti ilgalaikį atnaujinimą, patikrinkite
Dabar paaiškinkime jo veikimo metodą. Ši „python“programa parašyta ant pip įdiegto paketo, pavadinto m2controller. Žemesnio lygio paketas siūlo atgalinio ryšio mechanizmą, kad kiekvienas gautas matavimo atnaujinimas suaktyvintų mūsų parašytą atgalinio ryšio funkciją ir išsaugotų duomenis vietiniame žurnalo faile. Žurnalo failo duomenų turinio formatas yra identiškas tam, kurį sukuria „Android“papildoma programa, todėl duomenų žurnalo failą, sukurtą naudojant „python“programą arba „andriod“papildomą programą, galima pakeisti.
Vartotojo „ctrl-C“signalas, užfiksuotas operacinės sistemos, perduodamas programai ir sustabdo begalinę ciklą, laukiant naujų matavimo duomenų.
Iki šiol žurnalo failas buvo sėkmingai sukurtas, ir ši programa iškvies analizės programą, kad ištirtų mūsų eksperimento rezultatus.
Čia yra du eksperimentai, o palyginimas rodo labai pastebimą skirtumą, pridedant 7 gramų įrenginį skirtingose vietose.
2 pav. Mes naudojame skalę, kad nustatytume faktinį šio „Bluetooth“matavimo aparato svorį.
3 paveiksle pavaizduota švytuoklė, kurioje 7 gramų įtaisas pritvirtintas prie apatinio švytuoklės galo. 4 pav. Sąrankos konfigūracija turi 7 gramų masę, esančią daug arčiau besisukančio šarnyro.
5 pav. Yra švytuoklės struktūros vaizdas iš arti.
4 žingsnis: duomenų analizė



„Bluetooth“matavimo aparatas sveria ~ 7 gramus, o tai sveria daug mažiau nei ~ 1,6 metro ilgio medinė lazda. Naudokite „standaus vienodo strypo“prielaidą, ir mes turime švytuoklės laikotarpio lygtį, T1 = 2*pi*(2l/3g)^0.5
Norėdami gauti gravitacijos konstantą, galime naudoti 9,8 m/s^2. Tačiau tikslesnę gravitacijos konstantą bet kurioje geografinėje vietovėje galima gauti iš šios žiniatinklio paslaugos:
www.wolframalpha.com/widgets/view.jsp?id=e…
San Francisko atveju jis yra 9,81278 m/s^2
Švytuoklės ilgis yra 64,5 colio
2*pi*kv.
Pažiūrėkime, ar tai atitinka mūsų eksperimentus.
Pirmajame eksperimente švytuoklės sąranka turi 7 gramų įtaisą, pritvirtintą prie apatinio švytuoklės galo. Mano žurnalo failą galima atsisiųsti iš:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Pervardykite jį į „PendulumTestData.txt“ir įdėkite į tą patį „python“analizės programos aplanką. Čia pateikiamas šaltinio kodo momentinis vaizdas.
#!/usr/bin/env python#-*-kodavimas: UTF-8-*-importuoti csv importuoti matplotlib.pyplot kaip plt plt.style.use ('seaborn-whitegrid') importuoti numpy kaip np iš datetime import data datetime, „timedelta“importuoja jūrų gėrybes kaip sns iš sklearn.cluster importas ############################ Ši funkcija atlieka duomenų failų analizės darbą ########### ############################################### ## def parseDataLogFile (duomenų rinkmenos pavadinimas): ###################################### ########################ištraukite duomenis kableliais atskirtų duomenų žurnalo faile (CSV) ir išsaugokite kiekvieno stulpelio turinį į vieną plūdės tipo kintamąjį ## ############################################### ############ su atvira (duomenų failo pavadinimas) kaip csvfile: readCSV = csv.reader (csvfile, delimiter = ',') timestampS = fAccelHwUnit_x = fAccelHwUnit_y = fAccelHwUnit_ [fGyroHwUnit_x = fGyroHwUnit_y = fGyroHwUnit_z = fMagHwUnit_x = fMagHwUnit_y = fMagHwUni t_z = fRPYdeg_r = fRPYdeg_p = fRPYdeg_y = eilutei „readCSV“: pabandykite: x = datos laikas.strptime ([0] eilutė. skilimas (',') [0], '%H:%M:%S.%f ') timestampS.append (laikas [1] [4:])) fAccelHwUnit_y.append (float ([2] eilutė)) fAccelHwUnit_z.append (float ([3] eilutė)) fGyroHwUnit_x.append (float ([4] eilutė)) fGyroHwUnit_y.append (float (eilutė [5])) fGyroHwUnit_z.append (float ([6] eilutė)) fMagHwUnit_x.append (float (eilutė [7])) fMagHwUnit_y.append (float (eilutė [8])) fMagHwUnit_z.append (float (row [9])) fRPYdeg_r.append (plūdė (eilutė [10])) fRPYdeg_p.append (plūdė (eilutė [11])) fRPYdeg_y.append (plūdė (eilutė [12])), išskyrus: praeiti timestampSS = np.asarray (laiko žymes) laiko žymes = laiko atspaudus - laiko žymes [0] fAccelHwUnit_x = np.asarray (fAccelHwUnit_x) fAccelHwUnit_y = np.asarray (fAccelHwUnit_y) fAccelHwUnit_z = np.asarray (fAccelHwUnit_z) fGyroHwUnit_x = np.asarray (fGyroHwUnit_x) fGyroHwUnit_y = np.asarray (fGyroHwUnit_y) fGyroH wUnit_z = np.asarray (fGyroHwUnit_z) fMagHwUnit_x = np.asarray (fMagHwUnit_x) fMagHwUnit_y = np.asarray (fMagHwUnit_y) fMagHwUnit_z = np.asarray (fMagHwUnit_z) fRPYdeg_r = np.asarray (fRPYdeg_r) fRPYdeg_p = np.asarray (fRPYdeg_p) fRPYdeg_p = fRPYdeg_p - np.rean (fRPYdeg_p) fRPYdeg_y = np.asarray (fRPYdeg_y)
################################################################
#mums reikia tikslaus mėginių ėmimo dažnio įvertinimo, kad būtų galima tiksliai apskaičiuoti svyravimo laikotarpį ########################## ############################# FsHz = getSamplingIntervalS (timestampS) ############### ####################################### Naudojimas pikio komponentas požiūrio pozicijos atskaitos sistemos išvestyje švytuoklės laikotarpio analizei ##################################### ############################ analy_timeSequence (timestampS, fRPYdeg_p, FsHz, 'pitch') ############################################### ####švytuoklės laikotarpio analizei naudokite „acceleromter“neapdoroto matavimo rezultatus ############################# ############################ analy_timeSequence (timestampS, fAccelHwUnit_x, FsHz, 'accel') ########### ############################################### ####švytuoklės laikotarpio analizei naudokite neapdorotą giroskopo matavimo išvestį ############################# ##### gyro ') print (' padaryta, sveikinu:-) ') plt.show () ############################### ################################# „Bluetooth“ryšio proceso metu yra reta tikimybė, kad duomenų paketas gali būti pamestam#mes naudojame K-vidurkį, kad izoliuotume 20 Hz matavimo duomenis iš pašalinių rodiklių, kuriuos sukėlė iškritęs paketas#pasinerti į „signalą ir sistemą, kad gautumėte daugiau informacijos“################ ######################## ################## (timestampS): plt.figure () sampleIntervalS = np.diff (timestampS) sns.distplot (sampleIntervalS) plt.ylabel ('histogram') plt.xlabel ('matavimo intervalas (-ai))) clusterCnt = 5 km = KMeans (n_clusters = clusterCnt) km.fit (sampleIntervalS.reshape (-1, 1)) centroids = km.cluster_centers_ elemCnt = Skaitliukas (km.labels_) atsiradimasCnt = ii diapazone (clusterCnt): esinimasCnt.append (elemCnt [ii]) FsHz = 1/centroidai [reiškinysCnt.index (maks. (ĮvykisCnt)))] grąžina FsHz
################################################################
#naudokite spektrometrą, ty trumpą laiką FFT, kad gautumėte dažnio komponentą, smailė yra geriausias mūsų švytuoklės svyravimo įvertinimas ######################## ######################################################## CMBBBB> #################################interi-kulpetnymiu:#Analize_timeSequence (timestampS, timeSeqData, FsHz, strComment): pav., (ax1, ax2) = plt.subplots (nrows = 2) ax1.plot (timestampS, timeSeqData, marker = 'o', markerfacecolor = 'blue', markersize = 2, color = 'dangaus mėlyna', linijos plotis = 1) ax1.set_title ("švytuoklės laiko domeno matavimas - %s" %strComment) ax1.set_xlabel ("atrankos laikas (antras)") ax1.set_ylabel (strComment); NFFT = 2048 # langų segmentų ilgis
Pxx, dažniai, dėžės, im = ax2.specgram (timeSeqData, NFFT = NFFT, Fs = FsHz, noverlap = NFFT/2)
ax2.set_title ("Spektrograma") ax2.set_xlabel ("pavyzdžiai") ax2.set_ylabel ("dažnis (Hz)");
# Metodas „specgram“grąžina 4 objektus. Jie yra:
# - Pxx: periodograma # - dažniai: dažnio vektorius # - dėžės: laiko dėžių centrai # - im: matplotlib.image. AxesImage egzempliorius, vaizduojantis brėžinio duomenis pkresult = np.where (Pxx == np.amax (Pxx)) oscFreqHz = freqs [pkresult [0] [0] print ('švytuoklės svyravimų dažnis (Hz) =%f, periodas (sek) =%f, įvertinimo duomenų šaltinis:%s'%(oscFreqHz, 1/oscFreqHz, strComment)) grąžina 1/oscFreqHz
################################################################
#jei šią programą vykdytume savarankiškai, ty, nesikvietę pendulum1.py,#nustatome numatytąjį analizuojamo žurnalo duomenų failo pavadinimą #################### ###################### ### ": defaultFilename = './PendulumTestData.txt' importuoti os.path, jei os.path.isfile (defaultFilename): parseDataLogFile (defaultFilename) else: print (" numatytasis žurnalo failas %s nėra " %defaultFilename)
Norėdami gauti ilgalaikį atnaujinimą, patikrinkite
Šaltinio kode yra išsamių komentarų, čia pateikiame aukšto lygio matematinio įvertinimo santrauką.
1) Pirmiausia perskaitome CSV failo turinį į kompiuterį, naudodami „python“paketą „csv“. Mes atliekame periodinius matavimus.
21: 34: 26.362, eam: 0, -128, 14464, -8, 144, -96, 2112, -1280, 1664, -0,5, -5,5, 40,5
21: 34: 26.373, eam: 128, 0, 14272, -8, 136, 40, 2112, -1280, 1664, -0,5, -6,5, 40,0
21: 34: 26.412, eam: 448, -64, 14208, -8, 136, 24, 2176, -1280, 1664, -0,5, -7,5, 40,5
21: 34: 26.462, eam: 448, -128, 14272, -8, 120, 16, 2176, -1280, 1664, -0,5, -8,0, 40,5
2) Kadangi matavimo dažnis yra toks kritinis ir tiesiogiai įveda švytuoklinio laikotarpio įvertinimo paklaidą, norime juos įvertinti. Mūsų vardinis matavimo intervalas yra 50 ms, ty 20 Hz. Visų matavimų vidurkis atrodo gerai, tačiau retkarčiais prarandame duomenų perdavimo paketą, atnaujinimo intervalas tampa 100 ms arba 150 ms,…
Jei nubraižysime šių duomenų atsiradimą, žr. 1 pav., Kaip žmogus, akies obuolio vertė gali būti 0,05 sek. Tačiau ar galime tai padaryti geriau?
Turime naudoti klasifikavimo metodą, kad pasirinktume tik gerus apskaičiavimo vidurkius. „Python“turi įrankių rinkinį, pavadintą „KMeans“, kuris padės mums suskirstyti grupes arba, pavyzdžiui, klasifikuoti. Šios sąvokos naudojamos daugelyje didelių duomenų ir AI sričių.
3) 2 pav. Yra du vaizdai. Viršutinis brėžinys yra mūsų svyravimo kampo matavimo laiko srities seka laipsniais. Remdamiesi x ašies laiko žyma sekundėje, mes galime perskaityti maždaug 22,5 ciklų per 50 sekundžių, o tai reiškia 2,22 sek. Švytuoklės laikotarpį. Ar yra koks nors būdas automatizuoti šį procesą ir gauti tikslesnį įvertinimą? Taip, galime naudoti matematinį įrankį, vadinamą spektrograma, kuris naudoja nedidelę matavimo duomenų dalį ir nurodo mums jų dažnį, žr. Tamsiausios linijos y ašies rodmuo yra švytuoklės virpesių dažnis. Būdama horizontali linija patvirtina, kad švytuoklės svyravimai viso eksperimento metu nepasikeitė. Atvirkštinė virpesių dažnio vertė yra švytuoklės virpesių periodas.
Galutinė programos ataskaita yra tekstinė santrauka:
švytuoklės svyravimas Dažnis (Hz) = 0,449224, periodas (sek) = 2,226059, įvertinimo duomenų šaltinis: žingsnis
Galime pastebėti, kad ankstesnis akies obuolio skaičiavimo rezultatas, 2,22 sek., Gana atitinka programos apskaičiuotą vertę.
Palyginti su 2,0962 (sek.) Teoriškai apskaičiuota verte, turime ~ 5% likusios klaidos. Kaip jų atsikratyti? Prisiminkite prielaidą „standus vienodas strypas“? Net 7 gramų papildomas svoris atrodo nereikšmingas, tai yra didžiausia likusios klaidos priežastis.
Dabar mes perkeliame įrenginį arti šarnyro. Norėdami pamatyti nuotrauką iš arti, žr. Ankstesnį veiksmą. Mano sukurtą žurnalo failą galima atsisiųsti čia:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Atlikite tuos pačius analizės veiksmus ir gausime 2.089867 periodą (sek.), Žr. 3 pav., Kuris yra beveik identiškas teorinei prognozei. Puiku!
Kadangi mes turime ne tik svyravimo kampo matavimą, bet ir giroskopinį bei akselerometro matavimą tuo pačiu greičiu. Atlikite tą pačią analizę kitiems dviem matavimams, mes gauname 4 ir 5 pav. Įvertinimai iš visų trijų matavimo šaltinių sutinka, o tai leidžia labiau pasitikėti mūsų eksperimento sėkme.
Štai rezultatas, kaip galutinė paleistos „python“programos išvestis:
švytuoklės svyravimas Dažnis (Hz) = 0,478499, periodas (sek.) = 2,089867, įvertinimo duomenų šaltinis: žingsnis
švytuoklės svyravimas Freq (Hz) = 0.478499, periodas (sek.) = 2.089867, įvertinimo duomenų šaltinis: accel
švytuoklės virpesiai Freq (Hz) = 0.478499, periodas (sek.) = 2.089867, įvertinimo duomenų šaltinis: giroskopas
Paskutinė šio žingsnio mintis, kaip įvertinimo rezultatai gali būti visiškai vienodi naudojant skirtingus įvesties duomenų šaltinius? Tai priešinga intuicija. Šį klausimą paliksiu skaitytojams. Štai užuomina: atminkite, kad svyravimų dažniui įvertinti naudojame trumpalaikį FFT? Skaitmeninėje srityje dažnio įvertinimas pateikiamas atskirose dažnio dėžėse, o ne kintančio skaičiaus įvertyje.
5 žingsnis: būsimo darbo rekomendacijos
Yra keletas būsimų darbo rekomendacijų kategorijų.
Ankstesniame žingsnyje mes sugebame sumažinti savo eksperimento klaidą nuo ~ 5% iki mažiau nei 1%, ar galime tai padaryti geriau? Pastebėjus, kad svyravimų dydis mažėja eksponentiškai, vienas iš veiksnių gali būti oro pasipriešinimas sukant svyruoklę. Norint sumažinti aerodinaminį pasipriešinimą, gali tekti pakeisti švytuoklės skerspjūvį, kad jis būtų racionalios formos.
Ar galime pritaikyti kintantį laiko padidėjimą, išmoktą naudojant adaptyvius filtrų metodus, kad išvestų pastovaus piko dydžio signalą. Tuo tarpu koreguokite išorinių jėgų silpnėjimą.
Vargu ar rasime ką nors paprastesnio už „paprastą harmoninį judėjimą“. Ar galime pasinaudoti švytuoklės analizės priemonėmis, kad galėtume analizuoti ką nors sudėtingesnio, sportinę veiklą, vandens raketų paleidimo seką ir pan.?
Laimingas įsilaužimas
Rekomenduojamas:
Gauso ir parabolės tyrimas eksperimentinės lempos šviesos srautams: 6 žingsniai

Gauso ir parabolės, kad ištirtų eksperimentinės lempos šviesos srautus: Sveiki visi kūrėjai ir šurmuliuojanti „Instructable“bendruomenė. Šį kartą „Merenel Research“suteiks jums gryną tyrimo problemą ir būdą, kaip ją išspręsti naudojant matematiką. pats, kai skaičiavau RGB LED lempos LED srautus
Modeliavimo tyrimas: 9 žingsniai
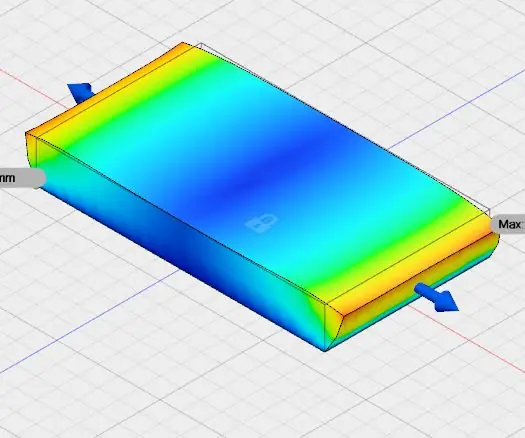
Modeliavimo tyrimas: Šioje instrukcijoje aš panaudojau „Autodesk“sintezę 360. Ši instrukcija skirta modeliavimo studijai. Čia panaudojau „auto desk fusion 360“modelį ir modeliavimo darbo vietą. Aš studijavau 10 N. dydžio išilginių jėgų modeliavimą
Paprasto keturių krypčių asociatyvaus talpyklos valdiklio VHDL dizainas: 4 žingsniai
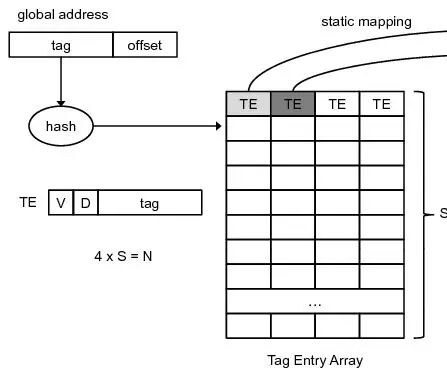
Paprasto keturių krypčių rinkinio asociatyvaus talpyklos valdiklio dizainas VHDL: Ankstesniame nurodyme pamatėme, kaip sukurti paprastą tiesioginį žemėlapio talpyklos valdiklį. Šį kartą žengiame žingsnį į priekį. Mes sukursime paprastą keturių krypčių asociatyvaus talpyklos valdiklį. Privalumas? Mažesnis praleidimo procentas, bet už perfo kainą
Paprasto talpyklos valdiklio VHDL dizainas: 4 žingsniai
Paprasto talpyklos valdiklio VHDL dizainas: Rašau šį nurodymą, nes man buvo šiek tiek sunku gauti tam tikrą nuorodinį VHDL kodą, kad išmokčiau ir pradėčiau kurti talpyklos valdiklį. Taigi aš pats nuo pat pradžių sukūriau talpyklos valdiklį ir sėkmingai išbandžiau jį FPGA. Turiu p
Paprasto VGA valdiklio dizainas VHDL ir „Verilog“: 5 žingsniai

Paprasto VGA valdiklio dizainas VHDL ir „Verilog“: Šioje instrukcijoje mes suprojektuosime paprastą VGA valdiklį RTL. VGA valdiklis yra skaitmeninė grandinė, skirta VGA ekranams valdyti. Jis nuskaitomas iš kadrų buferio (VGA atmintis), rodančio rodomą kadrą, ir sukuria reikiamą
