Blink Caos: Žemėlapis pagal atsitiktinį mirksėjimą: 5 žingsniai

2024 Autorius: John Day | [email protected]. Paskutinį kartą keistas: 2024-01-30 10:45

Este es un instructable para un generador de aleatoriedad, utilizando un mapa logístico, que ahora explico que es. Con el mapa logístico, se enciende y apaga un led de forma aleatoria. Este puede servir simplemente de ejemplo de como a través del caos se generan comportamientos aparentemente aleatorios. No se si es lo más práctico, pero es entretenido

1 žingsnis: Materiales

Ocupamos:

1. Arduino UNO
2. Bandomoji Lenta
3. Kabeliai
4. Vadovavo
5. Galia 10k omų

2 žingsnis: „Conexiones“

Tai reiškia, dainų tekstai: El led lo conectamos al pin 13 (pata larga) y a tierra (pata corta). Como estamos en el pin 13, ocupamos una resistencia.

El potenciametro, con contocos a "5V" la pata izquierda, a "GND" la pata derecha, y la del centro a A0.

Taip ir todo!

3 žingsnis: Žemėlapio logistika

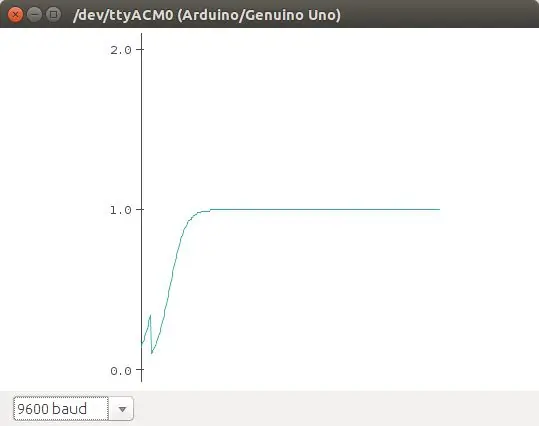
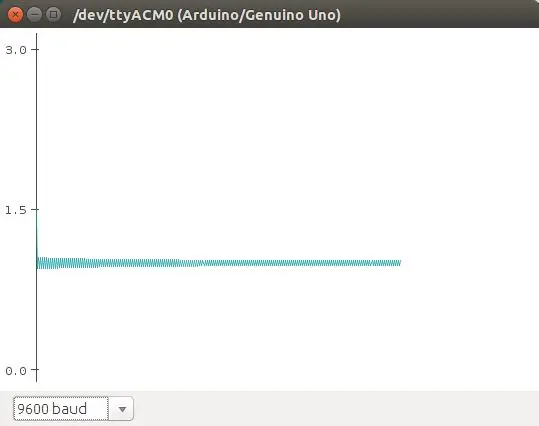
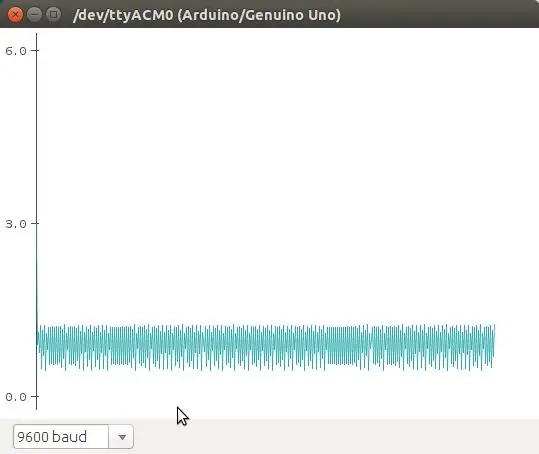
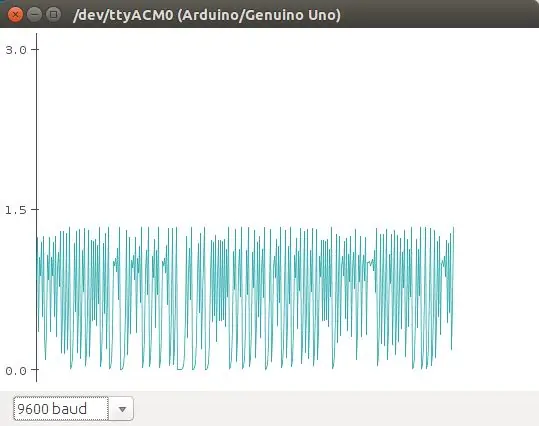
El mapa logístico es una ecuación que aprašo el crecimiento logístico de una población. Es una ecuación discreta en tiempo que va paso a paso, en tiempos discretos, re-calculando el tamaño de la población. Esta ecuación muestra como comportamiento caótico puede emerger de una ecuación tan simple. Fue popularizada autor Robert May en 1976. La ecuación:

n (t+1) = r * n (t) * (1 - n), aprašyti a la población en t+1, como una función de la población en t, multiplicado por su potencial biótico (como se reprodukcija), y un efecto denso -dependiente que se ievėti en el término (1 - n). Esta es la versión normalizada de la ecuación. Básicamente, debido al termino (1 - n), la población crece si n> 1, y decce n <1.

En este ejemplo vamos a utilizar como punto crítico cuando la población n> 1, que se encienda el led. El potencmetro se utiliza para cambiar los valores de r en la ecuación.

En las fotos se muestran algunos de los comportamientos que se obtienen de esa ecuación (graficados con el plotter de Arduino).

Pueden leer más sobre el mapa logístico en wikipedia

4 žingsnis: Código

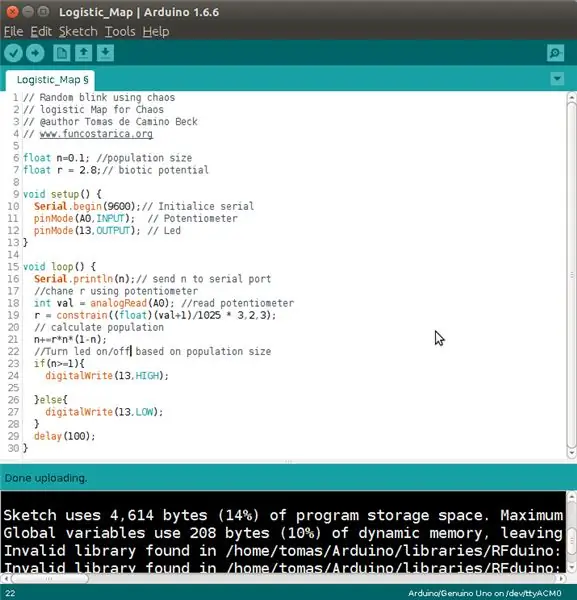
En el código lo importante está en el cuerpo main del program (loop), que es el que se utiliza para iterar sobre la ecuación del mapa logístico. En las líneas 6 y 7 se definen dos variables globales n para el tamaño de población y r para potencial biótico.

En la línea 18 se lee el potenciómetro, y en la 19, se convierte, primero a una escala de valor entre 0 y 1, y luego a un valor entre 0 y 3, aunque a eso se le aplica "constrain", para limitar los tipos de comportamiento que quiero con el potencimetro (hay varias maneras de hacerlo y esta probablemente no es la mejor)

De las líneas 23 a la 28 simplemente se päättää cuando prender el led.

Atsisiųskite el. Kodo para que lo puedan.

5 žingsnis: „Funcionando“

Como ven al mover el potencmetro pasamos de oscilaciones periódicas, es decir un blink intermitente con ciclos regulares, and uno caótico.

Esto se puede usar para tener un generador de ciclos de diferentes períodos, hasta llegar al caos.